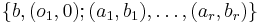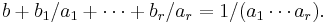Homology sphere
In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,
- H0(X,Z) = Z = Hn(X,Z)
and
- Hi(X,Z) = {0} for all other i.
Therefore X is a connected space, with one non-zero higher Betti number: bn. It does not follow that X is simply connected, only that its fundamental group is perfect (see Hurewicz theorem).
A rational homology sphere is defined similarly but using homology with rational coefficients.
Contents |
Poincaré homology sphere
The Poincaré homology sphere (also known as Poincaré dodecahedral space) is a particular example of a homology sphere. Being a spherical 3-manifold, it is the only homology 3-sphere (besides the 3-sphere itself) with a finite fundamental group. Its fundamental group is known as the binary icosahedral group and has order 120. This shows the Poincaré conjecture cannot be stated in homology terms alone.
Construction
A simple construction of this space begins with a dodecahedron. Each face of the dodecahedron is identified with its opposite face, using the minimal clockwise twist to line up the faces. Gluing each pair of opposite faces together using this identification yields a closed 3-manifold. (See Seifert–Weber space for a similar construction, using more "twist", that results in a hyperbolic 3-manifold.)
Alternatively, the Poincaré homology sphere can be constructed as the quotient space SO(3)/I where I is the icosahedral group (i.e. the rotational symmetry group of the regular icosahedron and dodecahedron, isomorphic to the alternating group A5). More intuitively, this means that the Poincaré homology sphere is the space of all geometrically distinguishable positions of an icosahedron (with fixed center and diameter) in Euclidean 3-space. One can also pass instead to the universal cover of SO(3) which can be realized as the group of unit quaternions and is homeomorphic to the 3-sphere. In this case, the Poincaré homology sphere is isomorphic to S3/Ĩ where Ĩ is the binary icosahedral group, the perfect double cover of I embedded in S3.
Another approach is by Dehn surgery. The Poincaré homology sphere results from +1 surgery on the right-handed trefoil knot.
Cosmology
In 2003, lack of structure on the largest scales (above 60 degrees) in the cosmic microwave background as observed for one year by the WMAP spacecraft led to the suggestion, by Jean-Pierre Luminet of the Observatoire de Paris and colleagues, that the shape of the Universe is a Poincaré sphere.[1][2] In 2008, astronomers found the best orientation on the sky for the model and confirmed some of the predictions of the model, using three years of observations by the WMAP spacecraft.[3] There is as yet no strong support for the correctness of the model, however.
Constructions and examples
- Surgery on a knot in the 3-sphere S3 with framing +1 or − 1 gives a homology sphere.
- More generally, surgery on a link gives a homology sphere whenever the matrix given by intersection numbers (off the diagonal) and framings (on the diagonal) has determinant +1 or −1.
- If p, q, and r are pairwise relatively prime positive integers then the link of the singularity xp + yq + zr = 0 (in other words, the intersection of a small 5-sphere around 0 with this complex surface) is a homology 3-sphere, called a Brieskorn 3-sphere Σ(p, q, r). It is homeomorphic to the standard 3-sphere if one of p, q, and r is 1, and Σ(2, 3, 5) is the Poincaré sphere.
- The connected sum of two oriented homology 3-spheres is a homology 3-sphere. A homology 3-sphere that cannot be written as a connected sum of two homology 3-spheres is called irreducible or prime, and every homology 3-sphere can be written as a connected sum of prime homology 3-spheres in an essentially unique way. (See Prime decomposition (3-manifold).)
- Suppose that a1, ..., ar are integers all at least 2 such that any two are coprime. Then the Seifert fiber space
- over the sphere with exceptional fibers of degrees a1, ..., ar is a homology sphere, where the b's are chosen so that
- (There is always a way to choose the b′s, and the homology sphere does not depend (up to isomorphism) on the choice of b′s.) If r is at most 2 this is just the usual 3-sphere; otherwise they are distinct non-trivial homology spheres. If the a′s are 2, 3, and 5 this gives the Poincaré sphere. If there are at least 3 a′s, not 2, 3, 5, then this is an acyclic homology 3-sphere with infinite fundamental group that has a Thurston geometry modeled on the universal cover of SL2(R).
Invariants
- The Rokhlin invariant is a Z/2Z valued invariant of homology 3-spheres.
- The Casson invariant is an integer valued invariant of homology 3-spheres, whose reduction mod 2 is the Rokhlin invariant.
Applications
If A is a homology 3-sphere not homeomorphic to the standard 3-sphere, then the suspension of A is an example of a 4-dimensional homology manifold that is not a topological manifold. The double suspension of A is homeomorphic to the standard 5-sphere, but its triangulation (induced by some triangulation of A) is not a PL manifold. In other words, this gives an example of a finite simplicial complex that is a topological manifold but not a PL manifold. (It is not a PL manifold because the link of a point is not always a 4-sphere.)
Galewski and Stern showed that all compact topological manifolds (without boundary) of dimension at least 5 are homeomorphic to simplicial complexes if and only if there is a homology 3 sphere Σ with Rokhlin invariant 1 such that the connected sum Σ#Σ of Σ with itself bounds a smooth acyclic 4-manifold. As of 2006[update] the existence of such a homology 3-sphere was an unsolved problem.
References
- ^ "Is the universe a dodecahedron?", article at PhysicsWorld.
- ^ Luminet, Jean-Pierre; Jeff Weeks, Alain Riazuelo, Roland Lehoucq, Jean-Phillipe Uzan (2003-10-09). "Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background". Nature (Nature) 425 (6958): 593–595. arXiv:astro-ph/0310253. Bibcode 2003Natur.425..593L. doi:10.1038/nature01944. PMID 14534579.
- ^ Roukema, Boudewijn; Zbigniew Buliński, Agnieszka Szaniewska, Nicolas E. Gaudin (2008). "A test of the Poincare dodecahedral space topology hypothesis with the WMAP CMB data". Astronomy and Astrophysics 482 (3): 747–753. arXiv:0801.0006. Bibcode 2008A&A...482..747L. doi:10.1051/0004-6361:20078777.
Selected reading
- Emmanuel Dror, Homology spheres, Israel Journal of Mathematics 15 (1973), 115–129. MR0328926
- David Galewski, Ronald Stern Classification of simplicial triangulations of topological manifolds, Annals of Mathematics 111 (1980), no. 1, pp. 1–34.
- Robion Kirby, Martin Scharlemann, Eight faces of the Poincaré homology 3-sphere. Geometric topology (Proc. Georgia Topology Conf., Athens, Ga., 1977), pp. 113–146, Academic Press, New York-London, 1979.
- Michel Kervaire, Smooth homology spheres and their fundamental groups, Transactions of the American Mathematical Society 144 (1969) 67–72. MR0253347
- Nikolai Saveliev, Invariants of Homology 3-Spheres, Encyclopaedia of Mathematical Sciences, vol 140. Low-Dimensional Topology, I. Springer-Verlag, Berlin, 2002. MR1941324 ISBN 3-540-43796-7
External links
- A 16-Vertex Triangulation of the Poincaré Homology 3-Sphere and Non-PL Spheres with Few Vertices by Anders Björner and Frank H. Lutz
- Lecture by David Gillman on The best picture of Poincare's homology sphere
- A cosmic hall of mirrors - physicsworld (26 Sep 2005)